期权策略（五）

BSM定价模型使用标的资产的现货价值作为得出期权价值的关键参数，而Black 76模型则用标的资产的远期/远期价值代替它。但这不过是一种数学上的替代，因此不应被视为根本性的差异。

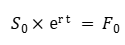
两个模型都假设基础资产具有对数正态分布，即基础资产只取正值（Black 76 并非为负利率设计）。然而，这两个模型在对基础资产变动性质的假设上存在关键差异——BSM假设基础资产遵循几何布朗运动，具有随时间变化的恒定漂移和波动率（遵循广义维纳过程），而Black 76假设基础资产的运动无漂移，其波动率是其绝对水平和时间的函数（类似于伊藤过程）。

作为符号表示，这可以表示为：对于一个现货价格为S，期货价格为F的基础资产，方程右边的项是标的资产的漂移和随机过程。

BSM

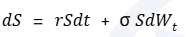
在BSM模型中，常数r和σ意味着衍生品的价值只依赖于其当前值和时间t。

Black-76

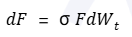
在Black-76模型中，公式里面的参数σ指的是期货价格的波动率，而不是标的指数本身的波动率。

这两种模型都假设零套利市场条件，并采用风险中性估值（概率测度），即风险偏好（对标的资产的风险厌恶程度）在定价期权时不发挥任何作用，所有未来的预期值都以无风险利率折现。这意味着今天远期的价值等于未来的预期价值（现货以无风险利率赚取）以无风险利率折现。

然而，BSM假设在任何时候都采用恒定的无风险利率，这对于定价利率期权是不合适的，因为标的资产本身会有其自身的波动性。由于Black模型对标的资产未来价值的期权定价，任何预期未来价值与实际远期的偏差都通过期货合约到期前的保证金调用得到抵消（这也是为什么标的资产的变动是无漂移的原因）。因此，即使我们考虑一个非风险中性世界（其中投资回报率高于或低于无风险利率），将变异性赋予标的资产的回报率r，也不会影响衍生品投资的现值/收益，前提是其未来现金流以相同的回报率折现，当然假设收益只在持有期t内是r的函数。

那么我们使用Black76模型来对春节后首个交易日的看涨期权与看跌期权合约对应的隐含波动率进行计算，除期权价格、期货价格以及行权价格以外的相关参数取值如下：

得到如下结果：

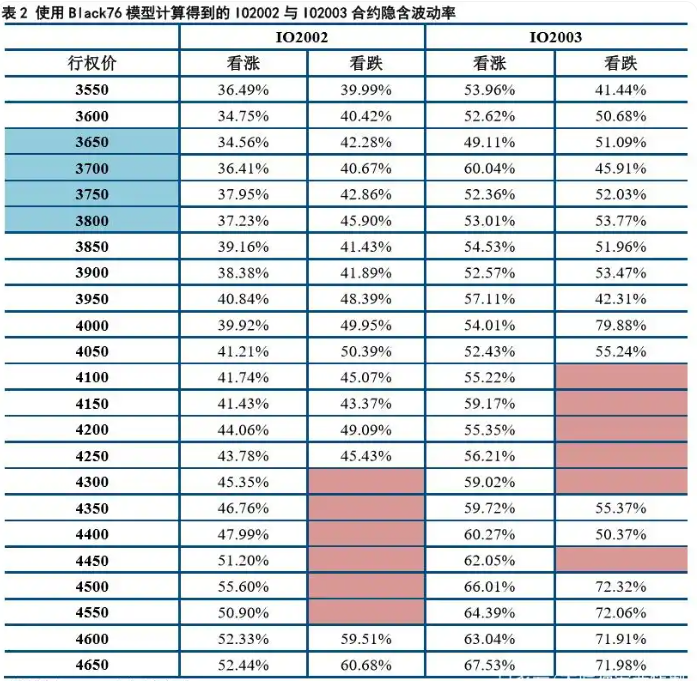
这里做一下说明，上面标红的空格部分没有数据，因为当日期权价格已经超出了理论上的下限值，导致计算不出隐含波动率。而我们之前根据Black-Scholes-Merton模型计算得到的各个合约在2020年2月3日当天的隐含波动率如下：

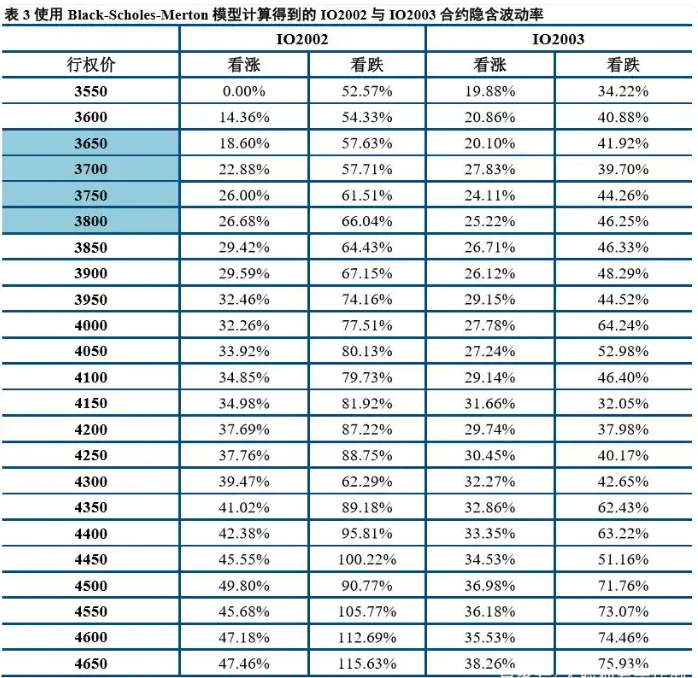
这里没有使用Black76模型进行IO2004合约隐含波动率的计算，因为当时股指期货2020年4月合约并没有上市。

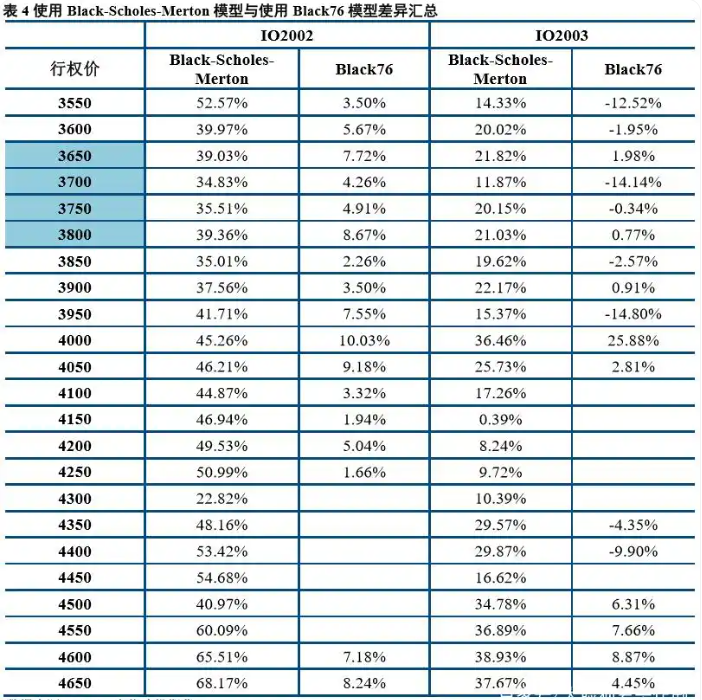
从上面的结果来看，使用Black76模型得到的看涨与看跌期权隐含波动率的差异相较于使用Black-Scholes-Merton 模型要小很多，这也和PCP平价公式的本质是相符合的，也可以过滤掉股指期货的升贴水对于隐含波动率的影响。

当然使用Black76模型来进行隐含波动率的计算时也存在一些问题。因为根据中国金融期货交易所的规则，沪深300股指期货的存续合约是当月、下月以及随后两个季月，一共是4期限的合约。而沪深300股指期权的存续合约则是包含了当月、后续两个月以及随后3个季月，一共是6个期限的合约。这样会导致我们使用Black76模型计算隐含波动率时会出现存在某个期限的沪深300股指期权合约，但是不存在相应期限的沪深300股指期货合约，这种情况下只能接受Black-Scholes-Merton模型作为一个备选项。